https://oj.leetcode.com/problems/lru-cache/
这个题目在leetcode连续很长时间都是热门题目,也听说面试的时候有遇见过的,今天下午就认真的做了一下。
Cache中的存储空间往往是有限的,当Cache中的存储块被用完,而需要把新的数据Load进Cache的时候,我们就需要设计一种良好的算法来完成数据块的替换。LRU的思想是基于“最近用到的数据被重用的概率比较早用到的大的多”这个设计规则来实现的。当空间不足的时候,就清除早期设置的而且不常用的数据。这也是操作系统中可能用到的页面置换算法,这段时间得关注一下操作系统中各种调度算法的实现,有时候概念很好理解,但是实际去写的时候就麻烦了。
其实这个题目思路并不是很难,关键是怎么找出最快的方法。开始我做的时候,就是简单的使用Python字典,对于每次命中的get操作,给这个key的”热度”加1,然后删除的时候找到最低的热度删除。因为Python的字典就是基于hash的,所以get操作很简单,主要是在set而且空间不足的时候,要去查找最低的热度值,这个操作明显是O(n)的时间复杂度,然后就超时了。其实后来认真想了一下,这个方法其实是错的,这个计算热度的话,只是看了数据的访问次数,而没有考虑到访问时间,是LFU算法了。
后来还尝试了几种别的办法,最终的到的提示是使用类似队列的结构来保存每个节点的”热度”,每次get或者set一个值的时候就把这个key放到最上面,然后在最底部的肯定就是最不常用的元素了。这样就避免了使用O(n)来查找那个元素。
#coding=utf-8
class LRUCache:
# @param capacity, an integer
def __init__(self, capacity):
self.capacity = capacity
self.cache = {}
self.history = []
# @return an integer
def _get(self, key):
value = self.cache.get(key, None)
if value:
self.history.remove(key)
self.history.append(key)
return value
def get(self, key):
cache = self._get(key)
if cache:
return cache
return -1
# @param key, an integer
# @param value, an integer
# @return nothing
def set(self, key, value):
cache = self._get(key)
#如果有这个kv 就更新一下 而且这个时候已经变换了history中的位置
if cache:
self.cache[key] = value
else:
if len(self.cache) >= self.capacity:
oldest = self.history[0]
self.cache.pop(oldest)
self.history.remove(oldest)
self.history.append(key)
self.cache[key] = value
这个题里面应该还有一个经常会搞错的地方,就是在判断get时候成功的时候,如果题目没有限定value的值都是正数,就不能使用if self.get(key) == -1来确定没有命中缓存了。因为有可能value的值就是-1。当然这个题目确定了value就是正数了。
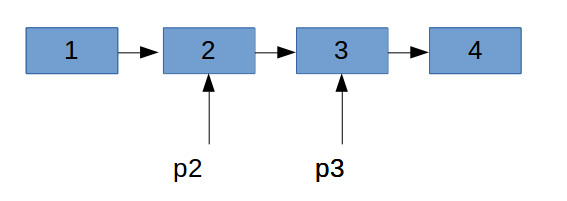
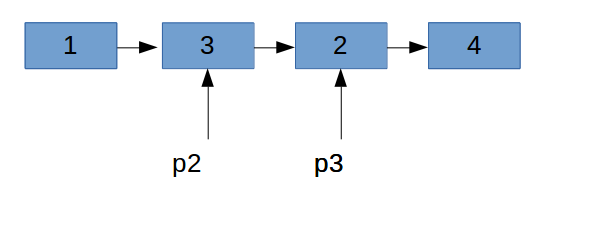
如果使用链表的话,结构上应该会更简单一点。set的时候使用c++ map查找,map的底层貌似是使用红黑树实现的,所以肯定低于O(n)的时间复杂度。但是找到这个值以后怎么将这个节点移到链表头上去呢,因为现在指针是指向的这个节点,我们如果知道它的上一个节点才能简单的删除。这个时候就会用到一个技巧,可以让当前节点和它后面的节点交换一下,然后再移动。这个技巧貌似在编程之美上提到过。如果从头来找这个节点又变成了O(n)了,同理,再单独维护一个尾指针就好了。当然如果使用双向链表就不存在这个问题了。
//交换两个值
tmp = p3 -> data
p3 -> data = p2 -> data
p2 -> data = tmp
//移动节点
p2 -> next = p3 -> next
p3 -> next = head

参考:http://www.cnblogs.com/dolphin0520/p/3749259.html
