微信、默默等查找附近的人最简单的方法就是遍历一遍，然后使用经纬度计算距离。计算公式是http://en.wikipedia.org/wiki/Haversine_formula
$$ havarsin(\frac{d}{R}) = haversin(l_{2} - l_{1}) + cos(l_{1})cos(l_{2})haversin(Δk) $$
其中
$$havarsin(θ) = sin^{2}(\frac{θ}{2}) = \frac{1 - cos(θ)}{2}$$
R是地球半径，$l_{1} l_{2}$是两点纬度，Δk是两点经度的差。
使用Python实现就是
from math import sin, asin, cos, radians, fabs, sqrt
EARTH_RADIUS=6371 # 地球平均半径，6371km
def hav(theta):
s = sin(theta / 2)
return s * s
def get_distance(lat0, lng0, lat1, lng1):
# 经纬度转换成弧度
lat0 = radians(lat0)
lat1 = radians(lat1)
lng0 = radians(lng0)
lng1 = radians(lng1)
dlng = fabs(lng0 - lng1)
dlat = fabs(lat0 - lat1)
h = hav(dlat) + cos(lat0) * cos(lat1) * hav(dlng)
distance = 2 * EARTH_RADIUS * asin(sqrt(h))
return distance
这样的话，每次搜索附近的人，都可以通过公式计算出来附近x km的经纬度范围，然后去数据库查询。这样的缺点就是每次生成的sql语句都不一样，很难缓存，毕竟附近的人不是特别精确的，只要两个人在同一个范围内就可以认为是在一起的。
目前常见的一个解决方案就是geohash，将经纬度映射到一个字符串上。
下面以(39.92324, 116.3906)为例，介绍一下geohash的编码算法。首先将纬度范围(-90, 90)平分成两个区间(-90, 0)、(0, 90)， 如果目标纬度位于前一个区间，则编码为0，否则编码为1。由于39.92324属于(0, 90)，所以取编码为1。然后再将(0, 90)分成 (0, 45), (45, 90)两个区间，而39.92324位于(0, 45)，所以编码为0。以此类推，直到精度符合要求为止，得到纬度编码为1011 1000 1100 0111 1001。经度也用同样的算法，对(-180, 180)依次细分，得到116.3906的编码为1101 0010 1100 0100 0100。
接下来将经度和纬度的编码合并，奇数位是纬度，偶数位是经度，得到编码 11100 11101 00100 01111 00000 01101 01011 00001。最后，用0-9、b-z（去掉a, i, l, o）这32个字母进行base32编码，得到(39.92324, 116.3906)的编码为wx4g0ec1。
http://code.google.com/p/python-geohash/有一个Python的geohash库，相关的api有
r = encode(50.231, 15.234, precision=5)
print r
print bbox(r)
print expand(r)
"""
u2fvf
{'s': 50.2294921875, 'e': 15.2490234375, 'w': 15.205078125, 'n': 50.2734375}
['u2fvc', 'u2fvg', 'u2fy1', 'u2fy4', 'u2fy5', 'u2fv9', 'u2fvd', 'u2fve', 'u2fvf']
"""
由上面的计算公式可以得到，编码长度为3的时候，一个编码能表示大约155km边长的正方形，4位的时候代表大约40km * 20km的矩形，5位的时候能代表5km * 5km的正方形。
还有一个误差对照表
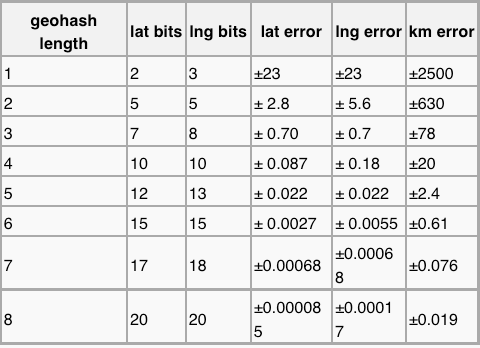
由于GeoHash是将区域划分为一个个规则矩形，并对每个矩形进行编码，目标点在靠近边界的时候，可能会出现：本区域内有一个距离稍远的，但是编码相同，而边界隔壁有一个距离很近的，但是编码不同。解决的思路很简单，我们查询时，除了使用定位点的GeoHash编码进行匹配外，还使用周围8个区域的GeoHash编码，这样可以避免这个问题，也就是上面的expand方法。
现有的GeoHash算法使用的是Peano空间填充曲线，这种曲线会产生突变，造成了编码虽然相似但距离可能相差很大的问题，因此在查询的时候，需要首先筛选GeoHash编码相似的POI点，然后进行实际距离计算。
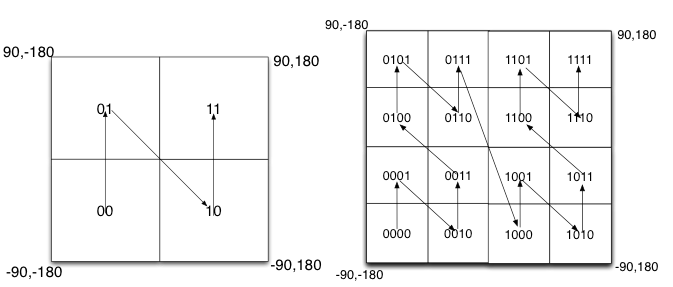Peano空间填充曲线最大的缺点就是突变性，有些编码相邻但距离却相差很远，比如0111与1000，编码是相邻的，但距离相差很大。
参考 http://blog.charlee.li/geohash-intro/
http://www.cnblogs.com/LBSer/p/3310455.html
http://www.zhihu.com/question/19596950
