一致性哈希学习
最近总是听到一致性哈希，但是不了解具体的技术详情。今天搜索了一下，记录下来。
应用场景
这里我先描述一个极其简单的业务场景：用4台Cache服务器缓存所有Object。
那么我将如何把一个Object映射至对应的Cache服务器呢？最简单的方法设置缓存规则
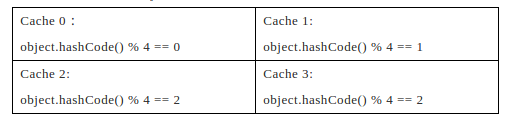看起来一切正常，考虑下面两种情况：
一：由于Cache3硬件损坏，所有Cache3上的缓存都失效了，需要把Cache3移除。
二：由于负载已经无法承担业务增涨，决定添加一台Cache服务器。
第一种情况下，这个节点的数据就完全不可用了. 当然你会说可以通过数据迁移呀, 恰恰难在数据迁移, 因为这时候挂了, 节点数变为3了, 对key取hash后再 mod 3 的话, 大部分的key对应的节点都要改. 这个时候只能整个集群的数据都重新迁移一遍才能达到效果；第二种情况也是一样，需要进行数据迁移。
一致性哈希算法简介
一致性哈希算法是在哈希算法基础上，提出的在动态变化的Cache环境中，哈希算法应该满足的4个适应条件。
平衡性(Balance) 平衡性是指Hash的结果能够尽可能分布均匀，充分利用所有缓存空间。
单调性(Monotonicity) 单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中，又有新的缓冲加入到系统中。哈希的结果应能够保证原有已分配的内容可以被映射到新的缓冲中去，而不会被映射到旧的缓冲集合中的其他缓冲区。
分散性(Spread) 分散性定义了分布式环境中，不同终端通过Hash过程将内容映射至缓存上时，因可见缓存不同，Hash结果不一致，相同的内容被映射至不同的缓冲区。
负载(Load) 负载是对分散性要求的另一个纬度。既然不同的终端可以将相同的内容映射到不同的缓冲区中，那么对于一个特定的缓冲区而言，也可能被不同的用户映射为不同的内容。
使用一致性哈希算法解决上述问题 一致性哈希算法采用一种新的方式来解决问题，不再仅仅依赖object.hashCode()本身，而且将Cache的配置也进行哈希运算。具体步骤如下：
- 首先求出每个Cache的哈希值，并将其配置到一个0~2^32的圆环区间上。
- 使用同样的方法求出需要存储对象的哈希值，也将其配置到这个圆环上。
- 从数据映射到的位置开始顺时针查找，将数据保存到找到的第一个Cache节点上。如果超过2^32仍然找不到Cache节点，就会保存到第一个Cache节点上。
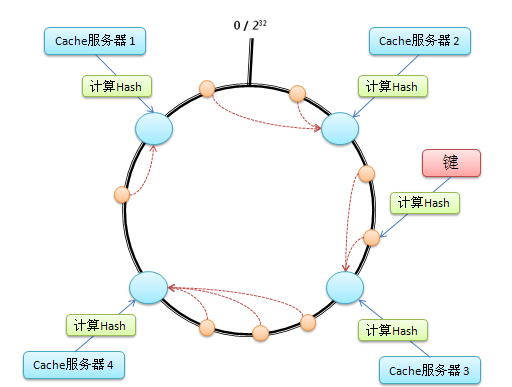
新增Cache服务器 假设在这个环形哈希空间中，Cache5被映射在Cache3和Cache4之间，那么受影响的将仅是沿Cache5逆时针遍历直到下一个Cache（Cache3）之间的对象（它们本来映射到Cache4上）。
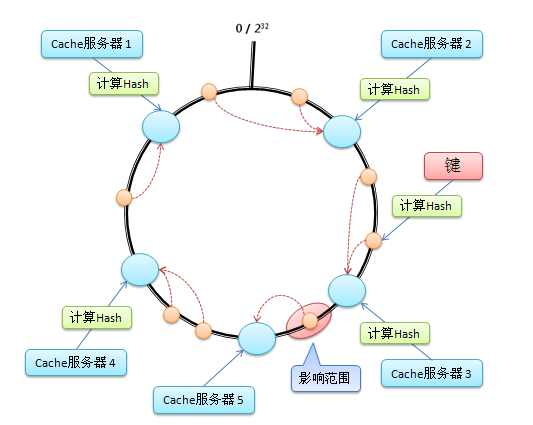
移除Cache服务器 假设在这个环形哈希空间中，Cache3被移除，那么受影响的将仅是沿Cache3逆时针遍历直到下一个Cache（Cache2）之间的对象（它们本来映射到Cache3上）。
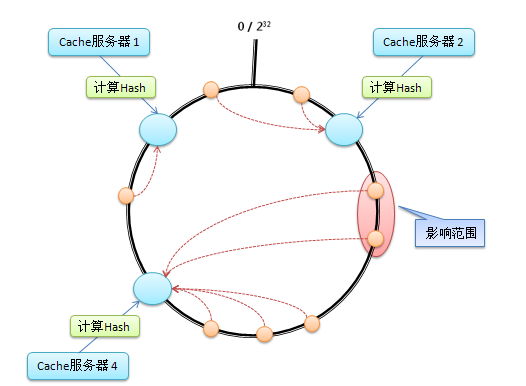
虚拟Cache服务器
考虑到哈希算法并不是保证绝对的平衡，尤其Cache较少的话，对象并不能被均匀的映射到 Cache上。为了解决这种情况，Consistent Hashing引入了“虚拟节点”的概念： “虚拟节点”是实际节点在环形空间的复制品，一个实际节点对应了若干个“虚拟节点”，这个对应个数也成为“复制个数”，“虚拟节点”在哈希空间中以哈希值排列。
仍以4台Cache服务器为例，在下图中看到，引入虚拟节点，并设置“复制个数”为2后，共有8个“虚拟节点”分部在环形区域上，缓解了映射不均的情况。
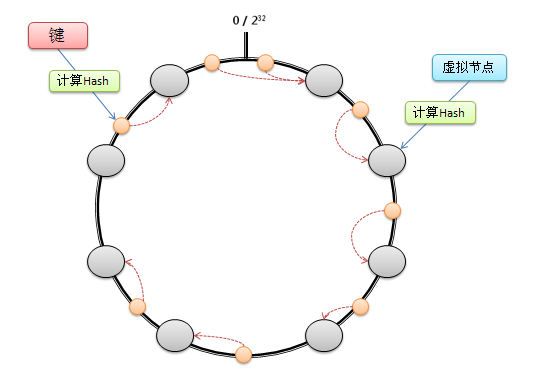
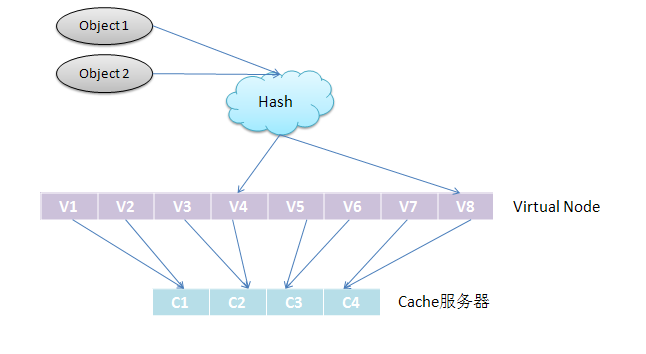
引入了“虚拟节点”后，映射关系就从【对象—>Cache服务器】转换成了【对象—>虚拟节点—> Cache服务器】。查询对象所在Cache服务器的映射关系如下图所示。
这里还有一个Python实现的代码
1import md5
2
3class HashRing(object):
4
5 def __init__(self, nodes=None, replicas=3):
6 """Manages a hash ring.
7
8 `nodes` is a list of objects that have a proper __str__ representation.
9 `replicas` indicates how many virtual points should be used pr. node,
10 replicas are required to improve the distribution.
11 """
12 self.replicas = replicas
13
14 self.ring = dict()
15 self._sorted_keys = []
16
17 if nodes:
18 for node in nodes:
19 self.add_node(node)
20
21 def add_node(self, node):
22 """Adds a `node` to the hash ring (including a number of replicas).
23 """
24 for i in xrange(0, self.replicas):
25 key = self.gen_key('%s:%s' % (node, i))
26 self.ring[key] = node
27 self._sorted_keys.append(key)
28
29 self._sorted_keys.sort()
30
31 def remove_node(self, node):
32 """Removes `node` from the hash ring and its replicas.
33 """
34 for i in xrange(0, self.replicas):
35 key = self.gen_key('%s:%s' % (node, i))
36 del self.ring[key]
37 self._sorted_keys.remove(key)
38
39 def get_node(self, string_key):
40 """Given a string key a corresponding node in the hash ring is returned.
41
42 If the hash ring is empty, `None` is returned.
43 """
44 return self.get_node_pos(string_key)[0]
45
46 def get_node_pos(self, string_key):
47 """Given a string key a corresponding node in the hash ring is returned
48 along with it's position in the ring.
49
50 If the hash ring is empty, (`None`, `None`) is returned.
51 """
52 if not self.ring:
53 return None, None
54
55 key = self.gen_key(string_key)
56
57 nodes = self._sorted_keys
58 for i in xrange(0, len(nodes)):
59 node = nodes[i]
60 if key <= node:
61 return self.ring[node], i
62
63 return self.ring[nodes[0]], 0
64
65 def get_nodes(self, string_key):
66 """Given a string key it returns the nodes as a generator that can hold the key.
67
68 The generator is never ending and iterates through the ring
69 starting at the correct position.
70 """
71 if not self.ring:
72 yield None, None
73
74 node, pos = self.get_node_pos(string_key)
75 for key in self._sorted_keys[pos:]:
76 yield self.ring[key]
77
78 while True:
79 for key in self._sorted_keys:
80 yield self.ring[key]
81
82 def gen_key(self, key):
83 """Given a string key it returns a long value,
84 this long value represents a place on the hash ring.
85
86 md5 is currently used because it mixes well.
87 """
88 m = md5.new()
89 m.update(key)
90 return long(m.hexdigest(), 16)
对于上面的代码我的看法是能比较清楚的解析一致性哈希的原理，但是实际使用的时候可能存在一些问题，比如md5算法效率问题，保存缓存节点的sorted_keys查找的时候的O(n)时间复杂度问题。
参考： http://blog.csdn.net/x15594/article/details/6270242 http://amix.dk/blog/post/19367
